Mayo

Clase #5

Martes 3 de Mayo del 2016

• Recta determinada por dos planos

Se halla teniendo las ecuaciones de dichos planos.

                           

• Ecuación del haz de los planos 

Es el conjunto de planos que pasa por una misma recta.

         

           

• Angulo entre dos planos 

                

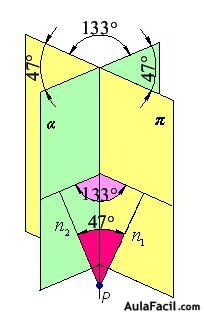
• Ecuación vectorial de la superficie esférica 

        

Para hallar dicha ecuación, solo se necesita conocer las coordenadas del centro de la superficie esférica, además de su radio, y se podrá plantear la ecuación de la siguiente manera:

• Cilindros y superficies cuadráticas

 

Clase #6

Jueves 5 de Mayo del 2016

Análisis gráficos de superficies

1.- Intersección de la superficie con los ejes coordenados

      Sea con el eje OX, OY, o OZ.

2.-Intersección de la superficie con los planos coordenados

     Sea el plano XOY, XOZ o YOZ.

3.-Intersección de la superficie con los planos paralelos a los ejes coordenado

4.-Bosquejo de la gráfica de la superficie

     Ejemplos:

Clase #7

Martes 10 de Mayo del 2016

Prueba Escrita #1

Clase #8

Jueves 12 de Mayo del 2016

• Funciones Vectoriales de variable real.

Las funciones vectoriales, también conocidas con el nombre de funciones valoradas vectoriales, son funciones matemáticas cuyo dominio es un conjunto de números reales y su rango es un conjunto infinito de vectores dimensionales. La notación convencional para tal función es,



De la ecuación anterior está claro que el rango de tal función es R3 o Rm. La interpretación de esta oración sería que la función está asociada con tres o más funciones de variables reales f1, f2,f3 … fm. Por tanto, se puede escribir de tal manera que,

Dominio:



Rango:



Decimos que una función es vectorial cuando tiene la forma:

Clase #9

Martes 17 de Mayo del 2016

• Operaciones con Funciones Vectoriales: 

Se nos enseñó las principales operaciones que se pueden realizar utilizando funciones vectoriales y son:

(F + G)(t) = F(t) + G(t); para todo t elemento de la intersección de los dominios de F y G
(x.F)(t) = x.F(t); donde x es elemento de los reales y t es elemento del dominio de F
(Foh)(t) = F(h1(t)); F(h2(t));...; F(hn(t)); para todo t elemento del dominio de F


Donde F y G son funciones definidas en los reales, se pueden realizar otras operaciones entre funciones vectoriales tales como producto punto y producto cruz.

• Limites y Continuidad

   Si r(t) = (f(t), g(t), h(t)), entonces:

• Existirá el límite de una función vectorial siempre y cuando existan los límites de cada una de sus funciones componentes.
• Los límites de funciones vectoriales siguen las reglas y cumplen las mismas propiedades de los límites de las funciones reales escalares.
• Una función r(t) será continua en un punto a, solo si el límite de r(t) cuando t tiende a "a" es igual a r(a).
• r(t) es continua en "a", si y solo si f(t), g(t), h(t) son continuas cuando t tiende a "a".
• Ejemplo:                      

Clase #10

Jueves 19 de Mayo del 2016

• Interpretación física de la derivada:

F'(to) se considera el vector tangente c en to. F'(to) = V(to), vector velocidad, el modulo de F'(to) representa la velocidad escalar.

El vector F'(to), cuando es diferente de cero determina la recta tangente a la recta tangente a la curva c: L = {F(to) + t.F(to); para todo t elemento de los reales}.

• Integración de Funciones Vectoriales:

        

• Longitud de curva y Arco de curva:

     

Clase #11

Martes 24 de Mayo del 2016

• Curvatura

          Vector Curvatura



Un círculo de radio l/ k es formado por la recta en caso que tenga la misma curvatura en todos sus puntos.En cada uno de los puntos la curvatura puede ser calculada como:

• Curvatura de flexión:

       

• Curvatura de torsión

        

• Radio de curvatura

        

Clase #12

Jueves 26 de Mayo del 2016

• Vector normal unitario 

Este vector es utilizado para encontrar la ecuación de la recta normal a la curva en un punto dado. Para calcularlo se utiliza la siguiente ecuación.




El vector normal unitario también puede ser calculado gracias a un teorema con la siguiente ecuación.

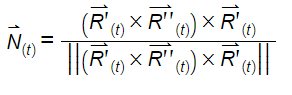
• Vector binormal 

El vector binormal, es un vector perpendicular al vector tangente unitario y al vector normal unitario. Para calcularlo se puede utilizar cualquiera de las siguientes fórmulas.



Como se dijo anteriormente, al ser estos 3 vectores perpendiculares entre si, al conocer dos de ellos se puede calcular el restante utilizando el producto cruz (X) y aplicando la regla de la mano derecha. Conceptos estudiados en álgebra vectorial.

• Triedro móvil y su aplicación: 

El triedro móvil es la unión de los tres vectores unitarios estudiados anteriormente (tangencial, normal y binormal). Se denomina móvil ya que estos vectores pueden ser encontrados en cualquier punto del dominio de la función vectorial.

Triedro móvil en t es:{ T(t), N(t), B(t) }

Aplicación: 

1. Plano Osculador. Es el plano que contiene al vector tangente y el vector normal a la curva. En este plano se encuentra contenida la velocidad y la aceleración, estudiadas anteriormente. 
2. Plano Normal Principal: Es el plano que contiene al vector binormal y normal unitario. 
3. Plano rectificador: Es el plano que contiene al vector binormal y tangente unitario. 

Video Explicativo:

• Funciones de varias variables: 

En la función dada por z = f(x,y); x y y son las variables independientes y z es la variable dependiente.

Pueden darse definiciones similares para las funciones de tres, cuatro o n variables donde los dominios consisten en tríadas (x1, x2, x3), tétradas (x1, x2, x3, x4) y adas (x1, x2, . . ., xn). En todos los casos, el rango es un conjunto de números reales.

Para comprender cual es el dominio de la función es necesario (siempre que sea posible) realizar los siguientes puntos.

Análisis matemático: Encontrar los puntos asintóticos donde la función no está definida.
Análisis gráfico: En caso de ser posible se debe graficar el dominio de la función.
Análisis descriptivo: En caso de ser posible, expresar con palabras lo encontrado anteriormente.

• Ecuación del plano osculador (PO): B1(X - Xo) + B2(Y - Yo) + B3(Z - Zo) = 0

• Ecuación del plano normal (PNP): T1(X - Xo) + T2(Y - Yo) + T3(Z - Zo) = 0

• Ecuación del plano rectificador (PR): N1(X - Xo) + N2(Y - Yo) + N3(Z - Zo) = 0

• Ecuación recta tangente (RT): (X - Xo)/T1 = (Y - Yo)/T2 = (Z - Zo)/T3

• Ecuación recta binormal (RB): (X - Xo)/ B1 = (Y - Yo)/ B2 = (Z - Zo)/ B3

• Ecuación recta normal principal (RNP): (X - Xo)/ N1 = (Y - Yo)/ N2 = (Z - Zo)/ N3

Clase #13

Martes 31 de Mayo del 2016

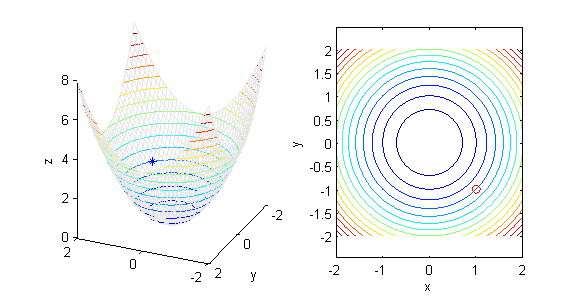
• Graficas y Curvas de nivel

Si f es una función de dos variables con dominio D, entonces la gráfica de f es el conjunto de todos los puntos (x,y,z), tal que z=f(x,y) y (x,y) está en el dominio. La gráfica es una superficie en R3.

• Curvas de nivel

Las curvas de nivel de una función f de dos variables son las curvas cuyas ecuaciones son f(x,y)=k, donde k es una constante.