Junio

Clase #14

Martes 5 de Junio del 2016

• Curvas de nivel

Una curva es una línea continua de una dimensión, que varía de dirección paulatinamente. Ejemplos sencillos de curvas cerradas son la elipse o la circunferencia, y de curvas abiertas la parábola y la hipérbola. 
en fin, una curva es una linea que hace firuletes en un espacio vectorial.

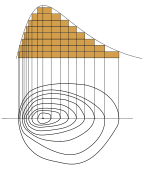
Una curva de nivel es aquella línea que en un mapa une todos los puntos que tienen igualdad de condiciones y de altitud. Las curvas de nivel suelen imprimirse en los mapas en color siena para el terreno y en azul para los glaciares y las profundidades marinas.

• Limites y Continuidad

El estudio de límites y continuidad en funciones de varias variables, y más adelante el de su diferenciabilidad, se reduce al estudio de sus funciones componentes. Para calcular límites lo podemos hacer por componentes, y la continuidad se tiene si y solo si se tiene continuidad en cada una de las componentes. Por tanto lo más importante es saber trabajar sobre las funciones componentes que en general son lo que denominamos campos escalares. Así pues el estudio de los campos escalares es fundamental. Tras algunas nociones básicas y definiciones nos centraremos en el estudio de técnicas sobre cálculo de límites de campos escalares y aplicaremos estas al estudio de la continuidad.

Clase #15

Martes 7 de Junio del 2016

• Continuación de Limites y Continuidad

Clase #16

Jueves 9 de Junio del 2016

• Derivadas Parciales

 Sea una función de dos variables z = f(x, y), se definen las derivadas parciales:

(Una definición obvia si la comparamos con la derivada de una función de una variable)
Para la derivada de z "respecto de x" consideramos a la variable "y" como si fuera una constante, mientras que al hacer la derivada de z "respecto de y" consideramos a la variable "x" como si fuera constante.

• Interpretación de las Derivadas Parciales

Si la función es de dos variables, la noción de derivada parcial se puede interpretar geométricamente. Las derivadas parciales de una función f en el punto (a, b) no son más que derivadas de una función de una variable: la función cuya gráfica se obtiene como intersección de la superficie con los planos verticales x=a, y=b, en los casos de derivada parcial en la dirección del eje Y en la dirección del eje X, respectivamente.

• Derivación de Funciones Implícitas

Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:

x'=1.

En general y'≠1.

Por lo que omitiremos x' y dejaremos y'.

Clase #17

Martes 14 de Junio del 2016

• Derivada Direccional

• Gradiente

Se llama gradiente de una función z = f(x, y) en un punto P(x, y) al vector que sale del punto P y sus componentes son las derivadas parciales de la función en dicho punto

La derivada direccional se puede obtener como el producto escalar del gradiente por el vector unitario (si la función es diferenciable)

El gradiente indica el sentido de crecimiento más rápido de una función en un punto dado. La derivada direccional tiene su valor máximo en el sentido del gradiente y coincide con su módulo:

Clase #19

Martes 21 de Junio del 2016

• Derivada Parciales de Orden Superior

La definición es muy similar al límite de la definición de la derivada para una función de dos variables. Es importante considerar entonces que para una función de varias variables, no existe una sola derivada, pues la función cambia respecto a más de una.


Afortunadamente existe un procedimiento más simple para derivar parcialmente que utilizar el límite. Éste método consiste en considerar la variable respecto a la que no se deriva como constante. Es decir, si se deriva respecto a x, la variable y será constante y viceversa. Por ejemplo la siguiente función:



Las dos derivadas parciales son:



En el primer caso se toma a y como constante y en el segundo se toma a x como constante. Existen derivadas parciales más complicadas que otras, sin embargo se aplican siempre las mismas reglas de derivación que con funciones de dos variables.

Clase #20

Jueves 23 de Junio del 2016

• Aproximaciones Lineales

Clase #21

Martes 28 de Junio del 2016

• Regla de la Cadena

Clase #22

Jueves 30 de Junio del 2016

• Máximos y Mínimos

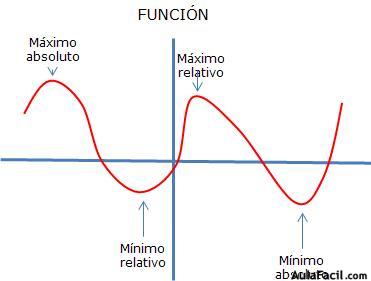
Una función de dos variables tiene un máximo relativo en (a,b) si f(x,y) <= (a,b), cuando (x,y) está cerca de (a,b) el valor f (a,b) recibe el nombre de VALOR MAXIMO RELATIVO. Si cumple que f(x,y) >= (a,b) cuando (x,y) está cerca de (a,b) el valor de f(a,b) recibe el nomre de VALOR MINIMO RELATIVO. Si estas condiciones de desigualdad se cumplen en todo el dominio de f(x,y) entoncs toman el nombre de maximos y minimos absolutos.

TEOREMA: si f tiene un maximo o un minimo relativo en (a,b) las derivadas parciales de primer orden existen ahí, entonces fx(a,b) = fy(a,b) = 0.

Si la funcion de dos variables presenta un maximo relativo y un minimo relativo en un mismo punto, se dice que dicho punto es un PUNTO DE SILLA.

REFERENCIAS

http://www.vitutor.com/

http://www.aulafacil.com/

http://www.lemat.unican.es/

http://www.derivadas.es/