Clase #1
Martes 19 de Abril del 2016
- Indicaciones generales.
- Geometría Analítica.
Clase #2
Sistema de funciones implícitas
La geometría analítica estudia las relaciones entre puntos, rectas, ángulos, distancias., de un modo algebraico, mediante fórmulas algebraicas y ecuaciones.
Tenemos 2 conjuntos A={1,2,3} , B={1,2}
AXB={(x,y)R2 / xeA ^ yeB}
AXB={(x,y)R2 / xeB ^ yeA}
....tenemos que AXB diferente de BXA
Caso hipotético
AXBXC={(x,y,Z)R3 / xeB ^ yeA^ zeC}
(x ─ a)2 + (y ─ b)2 = r2
La geometría analítica estudia las relaciones entre puntos, rectas, ángulos, distancias., de un modo algebraico, mediante fórmulas algebraicas y ecuaciones.
Tenemos 2 conjuntos A={1,2,3} , B={1,2}
AXB={(x,y)R2 / xeA ^ yeB}
AXB={(x,y)R2 / xeB ^ yeA}
....tenemos que AXB diferente de BXA
Caso hipotético
AXBXC={(x,y,Z)R3 / xeB ^ yeA^ zeC}
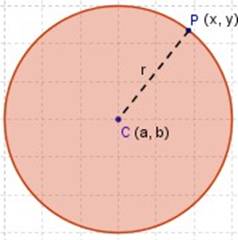
- Generalmente (dentro del Plano Cartesiano) diremos que ─para cualquier punto, P (x, y), de una circunferencia cuyo centro es el punto C (a, b) y con radio r─, la ecuación ordinaria es.
(x ─ a)2 + (y ─ b)2 = r2

Sistema de funciones implícitas

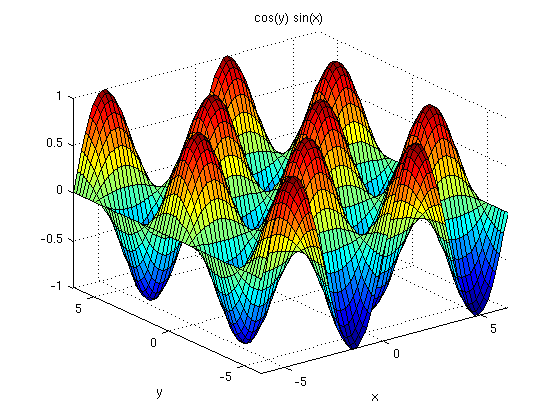
Cada una de las funciones implícitas representa una superficie por lo tanto la solución del sistema nos darán curvas. Si se tuvieran 3 funciones, la solución serían los puntos de intersección.
F(x,y,z)
G(x,y,z)
 La recta
La recta
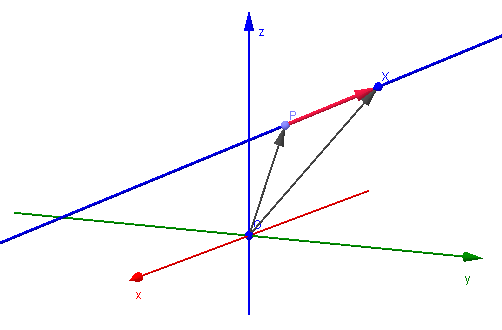
Donde la ecuación
a) Es la forma vectorial de la recta.
b) Es la ecuación paramétrica de la recta.
c) Es la ecuación canónica de la recta.
- Cada una de las funciones implícitas representa una curva por tanto la solución del sistema sera uno o mas puntos.
- En muchos casos se puede pasar de una forma a otra, pero algunas veces esto no es posible, o no siempre f(x,y)=0 representa a la función implícita de y=g(x).
- También existe f(x,y,z), una función explicita de 3 variables.


Cada una de las funciones implícitas representa una superficie por lo tanto la solución del sistema nos darán curvas. Si se tuvieran 3 funciones, la solución serían los puntos de intersección.
F(x,y,z)
G(x,y,z)


Donde la ecuación
a) Es la forma vectorial de la recta.
c) Es la ecuación canónica de la recta.
Si conocemos un punto de la recta y el vector director.

Si conocemos dos puntos de la recta.

Si conocemos dos puntos de la recta.

Clase #3
Martes 26 de Abril del 2016
El plano en el espacio




VIDEO INFORMATIVO
Clase #4
Jueves 28 de Abril del 2016
Normalización de le ecuación del plano
El plano en OpenGL se define mediante una función lineal de las tres coordenadas:
ax + by + cz + d = 0
Haciendo cero cada par de coordenadas, se ve que las intersecciones con los ejes son las indicadas en la figura. Por ejemplo: cuando y = z = 0, se pede despejar x = −d/a.
El versor normal al plano es el vector unitario que se obtiene normalizando el producto vectorial de dos vectores del plano, que no sean paralelos, por ejemplo el producto de dos aristas:
Se puede descartar el factor de escala (d*d)/abc para obtener, normalizando:
El plano en OpenGL se define mediante una función lineal de las tres coordenadas:
ax + by + cz + d = 0
Haciendo cero cada par de coordenadas, se ve que las intersecciones con los ejes son las indicadas en la figura. Por ejemplo: cuando y = z = 0, se pede despejar x = −d/a.
El versor normal al plano es el vector unitario que se obtiene normalizando el producto vectorial de dos vectores del plano, que no sean paralelos, por ejemplo el producto de dos aristas:
Se puede descartar el factor de escala (d*d)/abc para obtener, normalizando:
en el plano si el producto escalar da cero; no hace falta dividir.




No hay comentarios:
Publicar un comentario